Ejercicio 2

Hallar el vector X para una ecuación matricial:

A=[4 -2 -10;2 10 -12;-4 -6 16];
            b=[-10 32 -16]';
            x=A\b
            %%Otra opcion
            x1=inv(A)*b
            

            x =
            
                2.0000
                4.0000
                1.0000
            
            
            x1 =
            
                 2
                 4
                 1
            
Ejercicio 4
Hallar los autovalores y autovectores de la matriz A:
 
A=[0 1 -1;-6 -11 6;-6 -11 5];
            [X,D] = eig(A)
            T1= A*X
            T2= X*D
            
            X =
            
                0.7071   -0.2182   -0.0921
                0.0000   -0.4364   -0.5523
                0.7071   -0.8729   -0.8285
            
            
            D =
            
               -1.0000         0         0
                     0   -2.0000         0
                     0         0   -3.0000
            
            
            T1 =
            
               -0.7071    0.4364    0.2762
               -0.0000    0.8729    1.6570
               -0.7071    1.7457    2.4856
            
            
            T2 =
            
               -0.7071    0.4364    0.2762
               -0.0000    0.8729    1.6570
               -0.7071    1.7457    2.4856
            
Ejercicio 5
Para el siguiente circuito, determinar los voltajes de los nodos V1 y V2 y la potencia entregada por cada fuente:
 
Y=[1.5-2j -0.35+1.2j;-0.35+1.2j 0.9-1.6j];
            I=[30+40j;20+15j];
            V=Y\I;
            S=V.*conj(I);
            
%El potencial V1 en voltios vale:
            V1=V(1)
            
            V1 =
            
               3.5902 +35.0928i
            
            
%El potencial V2 en voltios vale:
            V2=V(2)
            
            V2 =
            
               6.0155 +36.2212i
            
            
%La potencia entregada por la fuente 1 en voltiamperios (VA) es:
            S1=S(1)
            
            S1 =
            
               1.5114e+03 + 9.0918e+02i
            
            
%La potencia entregada por la fuente 2 en voltiamperios (VA) es:
            S2=S(2)
            
            S2 =
            
               6.6363e+02 + 6.3419e+02i
            
      
            
            
Ejercicio 7
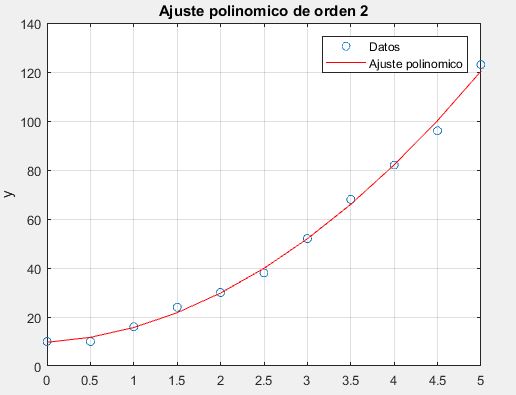
Ajustar un polinomio de orden 2 a los siguientes datos:
 
x= 0:0.5:5;
            y=[10 10 16 24 30 38 52 68 82 96 123];
            coeficientes=polyfit(x,y,2)
            yc=polyval(coeficientes,x);
            plot(x,y,'o',x,yc,'r');
            xlabel('x'),ylabel('y'),grid,title('Ajuste polinomico de orden 2')
            legend('Datos','Ajuste polinomico')
            
            coeficientes =
            
                4.0233    2.0107    9.6783
            
            
 
Ejercicio 8
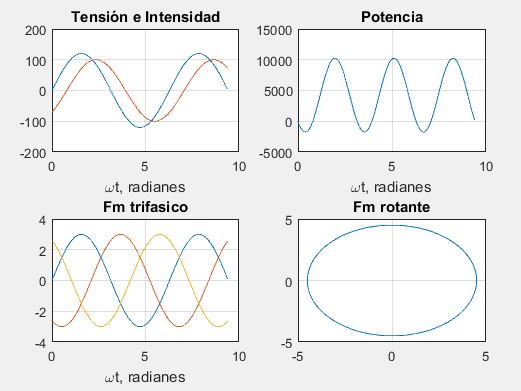
Partir la ventana Figure en cuatro particiones (2x2) y graficar las siguientes funciones para wt de 0 a 3pi en pasos de 0.05
Graficar v = 120 seno wt e i = 100 seno(wt - pi/4 ) en función de wt en la parte superior izquierda
Graficar p = vi en la parte superior izquierda
Para Fm = 3.0, graficar fa = Fm seno wt, fb = Fm seno(wt – 2 pi/3) y fc = Fm seno(wt – 4 pi/3) en función de wt en la parte inferior izquierda
Para fR = 3.0, construir un círculo de radio fR en la parte inferior derecha
wt=0:0.05:3*pi;
            figure(1)
            subplot(2,2,1)
            v=120*sin(wt);
            i=100*sin(wt-pi/4);
            plot(wt,v,wt,i)
            title('Tensión e Intensidad'),xlabel('\omegat, radianes')
            grid on
            
            subplot(2,2,2)
            p=v.*i;
            plot(wt,p)
            title('Potencia'),xlabel('\omegat, radianes')
            grid on
            
            subplot(2,2,3)
            Fm=3.0;
            fa=Fm*sin(wt);
            fb=Fm*sin(wt-2*pi/3);
            fc=Fm*sin(wt-4*pi/3);
            plot(wt,fa,wt,fb,wt,fc)
            title('Fm trifasico'),xlabel('\omegat, radianes')
            grid on
            
            subplot(2,2,4)
            fR= 3/2*Fm;
            plot(-fR*cos(wt),fR*sin(wt))
            title('Fm rotante')
            grid on
            

            
Ejercicio 13
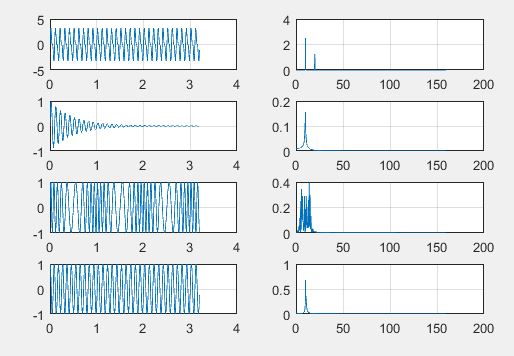
Tomando como base las condiciones del ejemplo de la transformada de Fourier de los apuntes (pág. 124), graficar para las siguientes señales la gráfica de la señal en el tiempo y la gráfica de la amplitud espectral en función de la frecuencia:
 
figure(5)
            k = 5; m = 10; fo = 10; Bo = 2.5; N = 2^m; T = 2^k/fo;
            ts = (0:N-1)*T/N;
            df = (0:N/2-1)/T;
            
            SampledSignal = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts);
            An = abs(fft(SampledSignal, N))/N;
            
            subplot(4,2,1)
            plot(ts, SampledSignal)
            grid on
            subplot(4,2,2)
            plot(df, 2*An(1:N/2))
            grid on
            
            SampledSignal1 = exp(-2*ts).*sin(2*pi*fo*ts);
            An1 = abs(fft(SampledSignal1, N))/N;
            
            subplot(4,2,3)
            plot(ts, SampledSignal1)
            grid on
            subplot(4,2,4)
            plot(df, 2*An1(1:N/2))
            grid on
            
            SampledSignal2 = sin(2*pi*fo*ts + 5*sin(2*pi*fo/10*ts));
            An2 = abs(fft(SampledSignal2, N))/N;
            
            subplot(4,2,5)
            plot(ts, SampledSignal2)
            grid on
            subplot(4,2,6)
            plot(df, 2*An2(1:N/2))
            grid on
            
            SampledSignal3 = sin(2*pi*fo*ts - 5*exp(-2*ts));
            An3 = abs(fft(SampledSignal3, N))/N;
            
            subplot(4,2,7)
            plot(ts, SampledSignal3)
            grid on
            subplot(4,2,8)
            plot(df, 2*An3(1:N/2))
            grid on